Fat-Tailed Distributions in Finance

In most classical financial models, we assume that asset prices follow a Geometric Brownian Motion (GBM). This implies that the log returns of the asset should be normally distributed.

However, empirical data shows that log returns often follow a fat-tailed (or heavy-tailed) distribution instead.

Comparison with the Normal Distribution

The tails of a standard normal distribution decay exponentially as:

\[\mathbb{P}(|X| > x) \sim \exp(-x^2).\]

In contrast, the empirical distribution of log returns places significantly more probability mass in the tails. That is:

Extreme events (both large gains and losses) occur more frequently than predicted by the normal distribution.
This results in a distribution with higher kurtosis (peaked center and fat tails).

Evidence from Q–Q Plots

Here is the Q-Q plot against a normal distribution. We observe:

Center of the plot follows the diagonal.
Tails deviate sharply:
- Left tail bends downward → more extreme negative returns.
- Right tail bends upward → more extreme positive returns.

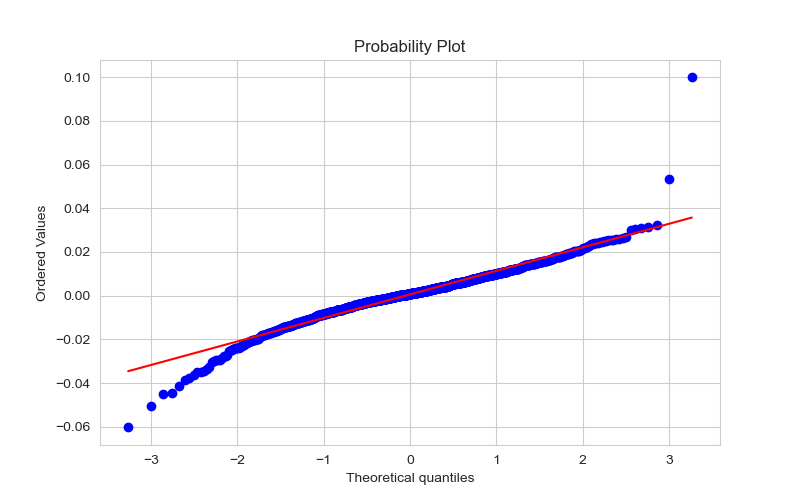
This characteristic “S-shape” or “bowtie shape” in the Q–Q plot is a signature of fat-tailed behavior.

Causes of Fat Tails in Financial Markets

Fat tails arise due to a variety of real-world factors not captured by simplistic models:

Cause	Explanation
Information shocks	Sudden unexpected news (e.g., geopolitical events, economic reports) can cause large price movements.
Liquidity crises	In illiquid markets, large orders can have disproportionate price impact, amplifying tail risk.
Feedback loops	Mechanisms like margin calls or stop-loss cascades can cause rapid price swings.
Herding behavior	Investors may imitate each other, amplifying moves in one direction.
Volatility clustering	Periods of low volatility are often followed by high-volatility bursts, leading to heavy tails (often modeled via GARCH).
Leverage and derivatives	Use of leverage magnifies gains and losses, increasing tail risk.